Self-organized criticality1-4 emerges in dynamical complex systems driven out of equilibrium, and characterizes a wide range of classical phenomena in physics, geology and biology. It is one of the most widely studied concepts in statistical physics and complexity science, yet it has never until now been identified in the full quantum regime – i.e., no system has ever been found entering the regime of 'quantum self-organized criticality'.
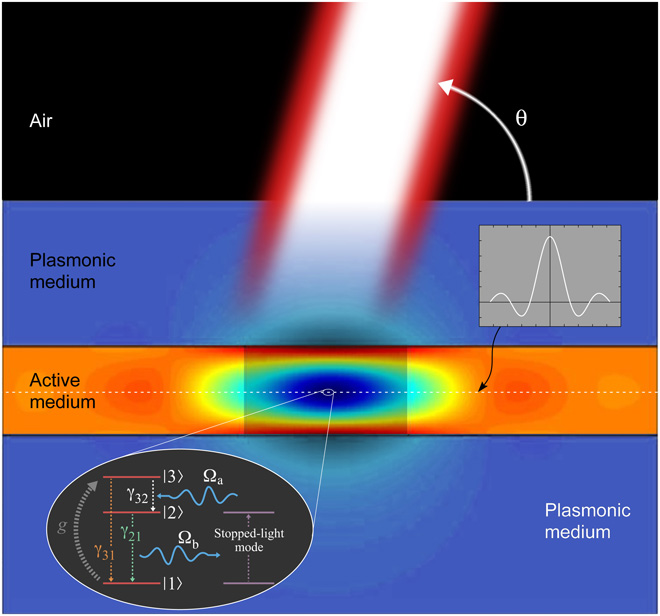
In this research theme, we study quantum-coherence controlled self-organized critical transitions observed in the light-localization behavior of coherence-driven nanophotonic configurations. Our systems are comprised of a gain-enhanced plasmonic heterostructures controlled by a coherent drive, wherein photons close to the stopped-light regime interact in the presence of the active nonlinearities, eventually synchronizing their dynamics. In such a system, on the basis of analytical and full-wave Maxwell-Bloch computations, we investigate the occurrence of quantum-coherence controlled self-organized criticality in the emergence of light localization arising from the synchronization of the photons. It is associated with two first-order phase transitions: one pertaining to the synchronization of the dynamics of the photons, and the second pertaining to an inversionless lasing transition by the coherent drive. The so-attained light localization, which is robust to dissipation, fluctuations and many-body interactions, exhibits scale-invariant power laws, as well as absence of finely-tuned control parameters. We have recently found5 that, in this nonequilibrium dynamical system, the effective critical "temperature" of the system drops to zero, whereupon one enters the quantum self-organized critical regime.
Our final, ongoing, objective is to identify a suitable system allowing one to enter and study the full dynamics of the quantum self-organized critical regime, on the basis of advanced (homemade) time-domain computational algorithms.